数据结构

简介

数据结构是计算机存储、组织数据的方式,算法是系统描述解决问题的策略。了解基本的数据结构和算法可以提高代码的性能和质量。

栈

栈的特点：先进后出； 正常插入，移除数组最后一项；

栈是一种遵从后进先出 (LIFO / Last In First Out) 原则的有序集合，它的结构类似如下：

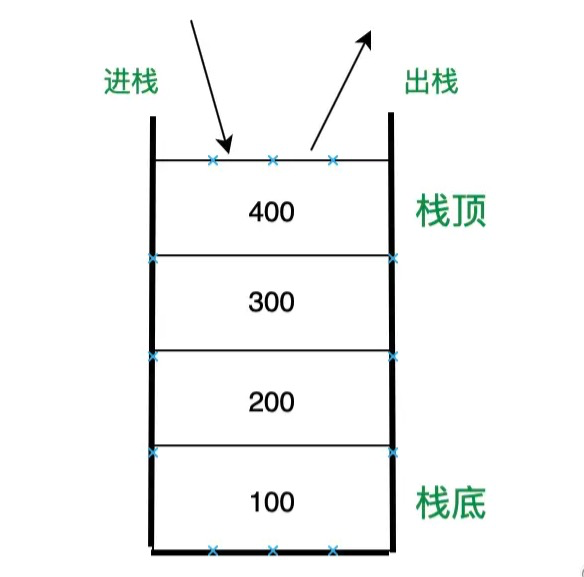
数组栈方法

• push() 可以接收任意数量的参数，把他们逐个添加到数组的末尾，返回修改后数组的长度；
• pop() 从数组末尾移除最后一项，返回移除的项；

栈的操作主要有： push(e) (进栈)、 pop() (出栈)、 isEmpty() (判断是否是空栈)、 size() (栈大小)，以及 clear() 清空栈，具体实现也很简单。

复杂度

查找：从栈头开始查找，时间复杂度为 O(n)

插入或删除：进栈与出栈的时间复杂度为 O(1)

class Stack {
  constructor() {
    this.items = [];
  }
  // 入栈
  push(element) {
    this.items.push(element);
  }
  // 出栈
  pop() {
    return this.items.pop();
  }
  // 清空栈
  clear() {
    this.items = [];
  }
  // 末位
  get peek() {
    return this.items[this.items.length - 1];
  }
  // 是否为空栈
  get isEmpty() {
    return !this.items.length;
  }
  // 长度
  get size() {
    return this.items.length;
  }
}
// 实例化一个栈
const stack = new Stack();
console.log(stack.isEmpty); // true

// 添加元素
stack.push(5);
stack.push(8);

// 读取属性再添加
console.log(stack.peek); // 8
stack.push(11);
console.log(stack.size); // 3
console.log(stack.isEmpty); // false

队列

队列：先进先出; 正常插入，移除数组第一项；

数组队列方法

• unshift() 向数组前端添加任意个项并返回新数组的长度；
• shift() 移除数组的第一项并返回该项 ；

class Queue { 
  constructor(items) { 
    this.items = items || []; 
  }
  enqueue(element) {
    this.items.unshift(element);
  }
  dequeue() {
    return this.items.shift();
  }
  front() {
    return this.items[0];
  }
  clear() {
    this.items = [];
  }
  print() {
    console.log(this.items.toString());
  }
  get size() {
    return this.items.length;
  }
  get isEmpty() {
    return !this.items.length;
  }
}

const queue = new Queue();
console.log(queue.isEmpty); // true

queue.enqueue("John");
queue.enqueue("Jack");
queue.enqueue("Camila");
console.log(queue.size); // 3
console.log(queue.isEmpty); // false
queue.dequeue();
queue.dequeue();
queue.dequeue();
console.log(queue.isEmpty); // true

字典

字典：类似对象，以key，value存贮值

class Dictionary { 
  constructor() { 
    this.items = {}; 
  }   
  set(key, value) {
    this.items[key] = value;
  }
  get(key) {
    return this.items[key];
  }
  remove(key) {
    delete this.items[key];
  }
  get keys() {
    return Object.keys(this.items);
  }
  get values() { // 在这里我们通过循环生成一个数组并输出
    return Object.keys(this.items).reduce((r, c, i) => {
      r.push(this.items[c]);
      return r;
    }, []);
  }
}
const dictionary = new Dictionary();
dictionary.set("Gandalf", "gandalf@email.com");
dictionary.set("John", "johnsnow@email.com");
dictionary.set("Tyrion", "tyrion@email.com");

console.log(dictionary);
console.log(dictionary.keys);
console.log(dictionary.values);
console.log(dictionary.items);

链表

• 链表: 存贮有序元素的集合;
• 但是不同于数组; 每个元素是一个存贮元素本身的节点和指向下一个元素引用组成;
• 要想访问链表中间的元素, 需要从起点开始遍历找到所需元素;

class Node {
  constructor(element) {
    this.element = element;
    this.next = null;
  }
}
// 链表
class LinkedList {
  constructor() {
    this.head = null;
    this.length = 0;
  }
  // 追加元素
  append(element) {
    const node = new Node(element);
    let current = null;
    if (this.head === null) {
      this.head = node;
    } else {
      current = this.head;
      while (current.next) {
        current = current.next;
      }
      current.next = node;
    }
    this.length++;
  }

  // 任意位置插入元素
  insert(position, element) {
    if (position >= 0 && position <= this.length) {
      const node = new Node(element);
      let current = this.head;
      let previous = null;
      let index = 0;
      if (position === 0) {
        this.head = node;
        node.next = current;
      } else {
        while (index++ < position) {
          previous = current;
          current = current.next;
        }
        node.next = current;
        previous.next = node;
      }
      this.length++;
      return true;
    }
    return false;
  }

  // 移除指定位置元素
  removeAt(position) {
    if (position > -1 && position < this.length) {// 检查越界值
      let current = this.head;
      let previous = null;
      let index = 0;
      if (position === 0) {
        this.head = current.next;
      } else {
        while (index++ < position) {
          previous = current;
          current = current.next;
        }
        previous.next = current.next;
      }
      this.length--;
      return current.element;
    }
    return null;
  }

  // 寻找元素下标
  findIndex(element) {
    let current = this.head;
    let index = -1;
    while (current) {
      if (element === current.element) {
        return index + 1;
      }
      index++;
      current = current.next;
    }
    return -1;
  }
  // 删除指定文档
  remove(element) {
    const index = this.findIndex(element);
    return this.removeAt(index);
  }
  isEmpty() {
    return !this.length;
  }
  size() {
    return this.length;
  }
  // 转为字符串
  toString() {
    let current = this.head;
    let string = "";
    while (current) {
      string += ` ${current.element}`;
      current = current.next;
    }
    return string;
  }
}
const linkedList = new LinkedList();

console.log(linkedList);
linkedList.append(2);
linkedList.append(6);
linkedList.append(24);
linkedList.append(152);

linkedList.insert(3, 18);
console.log(linkedList);
console.log(linkedList.findIndex(24));  

二叉树

特点：每个节点最多有两个子树的树结构

class NodeTree { 
  constructor(key) { 
    this.key = key; this.left = null; this.right = null; 
  } 
}
class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  insert(key) {
    const newNode = new NodeTree(key);
    const insertNode = (node, newNode) => {
      if (newNode.key < node.key) {
        if (node.left === null) {
          node.left = newNode;
        } else {
          insertNode(node.left, newNode);
        }
      } else {
        if (node.right === null) {
          node.right = newNode;
        } else {
          insertNode(node.right, newNode);
        }
      }
    };
    if (!this.root) {
      this.root = newNode;
    } else {
      insertNode(this.root, newNode);
    }
  }

  //访问树节点的三种方式:中序,先序,后序
  inOrderTraverse(callback) {
    const inOrderTraverseNode = (node, callback) => {
      if (node !== null) {
        inOrderTraverseNode(node.left, callback);
        callback(node.key);
        inOrderTraverseNode(node.right, callback);
      }
    };
    inOrderTraverseNode(this.root, callback);
  }

  min(node) {
    const minNode = node => {
      return node ? (node.left ? minNode(node.left) : node) : null;
    };
    return minNode(node || this.root);
  }

  max(node) {
    const maxNode = node => {
      return node ? (node.right ? maxNode(node.right) : node) : null;
    };
    return maxNode(node || this.root);
  }
}
const tree = new BinarySearchTree();
tree.insert(11);
tree.insert(7);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.inOrderTraverse(value => {
  console.log(value);
});

console.log(tree.min());
console.log(tree.max());

深度(DFS)/广度(BFS)遍历

对于算法来说 无非就是时间换空间 空间换时间

• 深度优先不需要记住所有的节点, 所以占用空间小, 而广度优先需要先记录所有的节点占用空间大；
• 深度优先有回溯的操作(没有路走了需要回头)所以相对而言时间会长一点；
• 深度优先采用的是堆栈的形式, 即先进后出；
• 广度优先则采用的是队列的形式, 即先进先出；

广度(BFS)遍历 题

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

输入:

   1
 /   \
2     3
 \
  5

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

用当前节点的值去拼接左右子树递归调用当前函数获得的所有路径。

也就是根节点拼上以左子树为根节点得到的路径，加上根节点拼上以右子树为根节点得到的所有路径。

直到叶子节点，仅仅返回包含当前节点的值的数组。

let binaryTreePaths = function (root) {
  let res = []
  if (!root) {
    return res
  }

  if (!root.left && !root.right) {
    return [`${root.val}`]
  }

  let leftPaths = binaryTreePaths(root.left)
  let rightPaths = binaryTreePaths(root.right)

  leftPaths.forEach((leftPath) => {
    res.push(`${root.val}->${leftPath}`)
  })
  rightPaths.forEach((rightPath) => {
    res.push(`${root.val}->${rightPath}`)
  })
  return res
}

学习方式

1. 分类刷题：很多第一次接触力扣的同学对于刷题的方法不太了解，有的人跟着题号刷，有的人跟着每日一题刷，但是这种漫无目的的刷题方式一般都会在中途某一天放弃，或者刷了很久但是却发现没什么沉淀。这里不啰嗦，直接点明一个所有大佬都推荐的刷题方法：把自己的学习阶段分散成几个时间段去刷不同分类的题型，比如第一周专门解链表相关题型，第二周专门解二叉树相关题型。这样你的知识会形成一个体系，通过一段时间的刻意练习把这个题型相关的知识点强化到你的脑海中，不容易遗忘。
2. 适当放弃：很多同学遇到一个难题，非得埋头钻研，干他 2 个小时。最后挫败感十足，久而久之可能就放弃了算法之路。要知道算法是个沉淀了几十年的领域，题解里的某个算法可能是某些教授研究很多年的心血，你想靠自己一个新手去想出来同等优秀的解法，岂不是想太多了。所以要学会适当放弃，一般来说，比较有目的性（面试）刷题的同学，他面对一道新的题目毫无头绪的话，会在 10 分钟之内直接放弃去看题解，然后记录下来，反复复习，直到这个解法成为自己的知识为止。这是效率最高的学习办法。
3. 接受自己是新手：没错，说的难听一点，接受自己不是天才这个现实。你在刷题的过程中会遇到很多困扰你的时候，比如相同的题型已经看过例题，稍微变了条件就解不出来。或者对于一个 easy 难度的题毫无头绪。或者甚至看不懂别人的题解（没错我经常）相信我，这很正常，不能说明你不适合学习算法，只能说明算法确实是一个博大精深的领域，把自己在其他领域的沉淀抛开来，接受自己是新手这个事实，多看题解，多请教别人。

分类大纲

1. 算法的复杂度分析。
2. 排序算法，以及他们的区别和优化。
3. 数组中的双指针、滑动窗口思想。
4. 利用 Map 和 Set 处理查找表问题。
5. 链表的各种问题。
6. 利用递归和迭代法解决二叉树问题。
7. 栈、队列、DFS、BFS。
8. 回溯法、贪心算法、动态规划。

算法

LRU算法

场景：浏览器缓存淘汰策略和Vue的keep-alive学习LRU算法

原理

LRU （ Least Recently Used ：最近最少使用 ）缓存淘汰策略，故名思义，就是根据数据的历史访问记录来进行淘汰数据，其核心思想是 如果数据最近被访问过，那么将来被访问的几率也更高 ，优先淘汰最近没有被访问到的数据。

图解

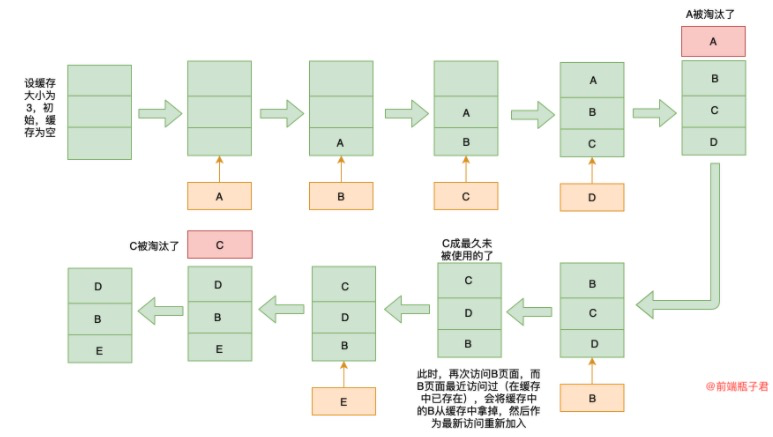
手写实现

vue 源码看 keep-alive 的实现

核心：

// 如果命中缓存，则从缓存中获取 vnode 的组件实例，并且调整 key 的顺序放入 keys 数组的末尾
if (cache[key]) {
  vnode.componentInstance = cache[key].componentInstance;
  remove(keys, key); // make current key freshest
  keys.push(key);
}
// 如果没有命中缓存,就把 vnode 放进缓存
else {
  cache[key] = vnode;
  keys.push(key); // prune oldest entry
  // 如果配置了 max 并且缓存的长度超过了 this.max，还要从缓存中删除第一个
  if (this.max && keys.length > parseInt(this.max)) {
    pruneCacheEntry(cache, keys[0], keys, this._vnode);
  }
}
vnode.data.keepAlive = true;// keepAlive标记位
}

完整：

export default {
  name: "keep-alive",
  abstract: true, // 抽象组件属性 ,它在组件实例建立父子关系的时候会被忽略,发生在 initLifecycle 的过程中
  props: {
    include: patternTypes, // 被缓存组件
    exclude: patternTypes,// 不被缓存组件
    max: [String, Number] // 指定缓存大小
  },
  created() {
    this.cache = Object.create(null);// 初始化用于存储缓存的 cache 对象
    this.keys = []; // 初始化用于存储VNode key值的 keys 数组
  },
  destroyed() {
    for (const key in this.cache) {
      pruneCacheEntry(this.cache, key, this.keys);// 删除所有缓存
    }
  },
  mounted() {
    // 监听缓存（include）/不缓存（exclude）组件的变化
    // 在变化时，重新调整 cache
    // pruneCache：遍历 cache，如果缓存的节点名称与传入的规则没有匹配上的话，就把这个节点从缓存中移除
    this.$watch("include", val => {
      pruneCache(this, name => matches(val, name));
    });
    this.$watch("exclude", val => {
      pruneCache(this, name => !matches(val, name));
    });
  },
  render() {
    // 获取第一个子元素的 vnode
    const slot = this.$slots.default;
    const vnode: VNode = getFirstComponentChild(slot);
    const componentOptions: ?VNodeComponentOptions =
      vnode && vnode.componentOptions;
    if (componentOptions) {
      // name 不在 inlcude 中或者在 exlude 中则直接返回 vnode，否则继续进行下一步
      // check pattern
      const name: ?string = getComponentName(componentOptions);
      const { include, exclude } = this;
      if (
        // not included
        (include && (!name || !matches(include, name))) ||
        // excluded
        (exclude && name && matches(exclude, name))
      ) {
        return vnode;
      }
      
      const { cache, keys } = this;
      // 获取键，优先获取组件的 name 字段，否则是组件的 tag
      const key: ?string =
        vnode.key == null
          ? // same constructor may get registered as different local components
            // so cid alone is not enough (#3269)
            componentOptions.Ctor.cid +
            (componentOptions.tag ? `::${componentOptions.tag}` : "")
          : vnode.key;
        
      // --------------------------------------------------
      // 下面就是 LRU 算法了，
      // 如果在缓存里有则调整，
      // 没有则放入（长度超过 max，则淘汰最近没有访问的）
      // --------------------------------------------------
      // 如果命中缓存，则从缓存中获取 vnode 的组件实例，并且调整 key 的顺序放入 keys 数组的末尾
      if (cache[key]) {
        vnode.componentInstance = cache[key].componentInstance;
        remove(keys, key); // make current key freshest
        keys.push(key);
      }
      // 如果没有命中缓存,就把 vnode 放进缓存
      else {
        cache[key] = vnode;
        keys.push(key); // prune oldest entry
        // 如果配置了 max 并且缓存的长度超过了 this.max，还要从缓存中删除第一个
        if (this.max && keys.length > parseInt(this.max)) {
          pruneCacheEntry(cache, keys[0], keys, this._vnode);
        }
      }
      vnode.data.keepAlive = true;// keepAlive标记位
    }
    return vnode || (slot && slot[0]);
  }
};

// 移除 key 缓存
function pruneCacheEntry (
  cache: VNodeCache,
  key: string,
  keys: Array<string>,
  current?: VNode
) {
  const cached = cache[key]
  if (cached && (!current || cached.tag !== current.tag)) {
    cached.componentInstance.$destroy()
  }
  cache[key] = null
  remove(keys, key)
}

// remove 方法（shared/util.js）
export function remove (arr: Array<any>, item: any): Array<any> | void {
  if (arr.length) {
    const index = arr.indexOf(item)
    if (index > -1) {
      return arr.splice(index, 1)
    }
  }
}

冒泡算法

详见10大经典排序算法

冒泡排序，选择排序，插入排序

1.终极篇

[1,2,3,4].sort((a, b) => a - b); // [1, 2,3,4],默认是升序
[1,2,3,4].sort((a, b) => b - a); // [4,3,2,1] 降序

sort是js内置的排序方法,参数为一个函数

2.开始篇

冒泡排序:

Array.prototype.bubleSort=function () {
  let arr=this,len = arr.length;
  for (let outer = len; outer >= 2; outer--) {
    for (let inner = 0; inner <= outer - 1; inner++) {
      if (arr[inner] > arr[inner + 1]) {//升序
        [arr[inner], arr[inner + 1]] = [arr[inner + 1], arr[inner]];
        console.log([arr[inner], arr[inner + 1]]);
      }
    }
  }
  return arr;
}
[1,2,3,4].bubleSort() //[1,2,3,4]    

选择排序

Array.prototype.selectSort=function () {
  let arr=this,len = arr.length;
  for (let i = 0, len = arr.length; i < len; i++) {
    for (let j = i, len = arr.length; j < len; j++) {
      if (arr[i] > arr[j]) {
        [arr[i], arr[j]] = [arr[j], arr[i]];
      }
    }
  }
  return arr;
}
[1,2,3,4].selectSort() //[1,2,3,4] 

斐波那契数列

特点：第三项等于前面两项之和; 1、1、2、3、5、8、13、21

递归实现：

function Fibonacci (n) {//测试：不使用尾递归
  if ( n <= 2 ) {return 1};
  return Fibonacci(n - 1) + Fibonacci(n - 2);// return 四则运算
}
// Fibonacci(10) // 89
// Fibonacci(100) // 超时
// Fibonacci(100) // 超时
console.log(Fibonacci(7));

function Fibonacci2 (n , f1 = 1 , f2 = 1) {//测试：使用尾递归
  if( n <= 2 ) {return f2};
  return Fibonacci2 (n - 1, f2, f1 + f2);
}
// Fibonacci2(100) // 573147844013817200000
// Fibonacci2(1000) // 7.0330367711422765e+208
// Fibonacci2(10000) // Infinity
console.log(Fibonacci2(7));

普通实现：

function fn(n){
       var num1 = 1, num2= 1, num3 = 0;
       for(var i=0;i<n-2;i++){
           num3 = num1+num2;
           num1 = num2;
           num2 = num3;
       }
       return num3;
   }
console.log(fn(7)) //13

动态规划

特点：通过全局规划,将大问题分割成小问题来取最优解

案例：最少硬币找零

• 美国有以下面额(硬币）：d1=1, d2=5, d3=10, d4=25
• 如果要找36美分的零钱，我们可以用1个25美分、1个10美分和1个便士（ 1美分)

class MinCoinChange {
  constructor(coins) {
    this.coins = coins
    this.cache = {}
  }
  makeChange(amount) {
    if (!amount) return []
    if (this.cache[amount]) return this.cache[amount]
    let min = [], newMin, newAmount
    this.coins.forEach(coin => {
      newAmount = amount - coin
      if (newAmount >= 0) {
        newMin = this.makeChange(newAmount)
      }
      if (newAmount >= 0 && 
          (newMin.length < min.length - 1 || !min.length) && 
          (newMin.length || !newAmount)) {
        min = [coin].concat(newMin)
      }
    })
    return (this.cache[amount] = min)
  }
}
const rninCoinChange = new MinCoinChange([1, 5, 10, 25])
console.log(rninCoinChange.makeChange(36))// [1, 10, 25]
const minCoinChange2 = new MinCoinChange([1, 3, 4])
console.log(minCoinChange2.makeChange(6))// [3, 3]

说明：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
  偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
  偷窃到的最高金额 = 2 + 9 + 1 = 12 。

动态规划的一个很重要的过程就是找到「状态」和「状态转移方程」，在这个问题里，设 i 是当前屋子的下标，状态就是 以 i 为起点偷窃的最大价值

在某一个房子面前，盗贼只有两种选择：偷或者不偷。

1. 偷的话，价值就是「当前房子的价值」+「下两个房子开始盗窃的最大价值」
2. 不偷的话，价值就是「下一个房子开始盗窃的最大价值」

在这两个值中，选择最大值记录在 dp[i]中，就得到了以 i 为起点所能偷窃的最大价值。。

动态规划的起手式，找基础状态，在这题中，以终点为起点的最大价值一定是最好找的，因为终点不可能再继续往后偷窃了，所以设 n 为房子的总数量， dp[n - 1] 就是 nums[n - 1]，小偷只能选择偷窃这个房子，而不能跳过去选择下一个不存在的房子。

那么就找到了动态规划的状态转移方程：

// 抢劫当前房子
robNow = nums[i] + dp[i + 2] // 「当前房子的价值」 + 「i + 2 下标房子为起点的最大价值」

// 不抢当前房子，抢下一个房子
robNext = dp[i + 1] //「i + 1 下标房子为起点的最大价值」

// 两者选择最大值
dp[i] = Math.max(robNow, robNext)

，并且从后往前求解。

function (nums) {
  if (!nums.length) {
    return 0;
  }
  let dp = [];

  for (let i = nums.length - 1; i >= 0; i--) {
    let robNow = nums[i] + (dp[i + 2] || 0)
    let robNext = dp[i + 1] || 0
    dp[i] = Math.max(robNow, robNext)
  }
  return dp[0];
};

最后返回 以 0 为起点开始打劫的最大价值 即可。

贪心算法

特点：通过最优解来解决问题 ； 用贪心算法来解决上面中的案例

function MinCoinChange(coins) {
  var coins = coins;
  var cache = {};
  this.makeChange = function(amount) {
    var change = [],
        total = 0;
    for (var i = coins.length; i >= 0; i--) {
      var coin = coins[i];
      while (total + coin <= amount) {
        change.push(coin);
        total += coin;
      }
    }
    return change;
  };
}

var minCoinChange = new MinCoinChange([1, 5, 10, 25]);
// console.log(minCoinChange.makeChange(36));//[ 25, 10, 1 ]
// console.log(minCoinChange.makeChange(34));//[ 25, 5, 1, 1, 1, 1 ]
console.log(minCoinChange.makeChange(6));//[ 5, 1 ]

说明：

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i ，都有一个胃口值 gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

注意：你可以假设胃口值为正。 一个小朋友最多只能拥有一块饼干。

示例 1:
输入: [1,2,3], [1,1]
输出: 1

解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:
输入: [1,2], [1,2,3]
输出: 2

解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

把饼干和孩子的需求都排序好，然后从最小的饼干分配给需求最小的孩子开始，不断的尝试新的饼干和新的孩子，这样能保证每个分给孩子的饼干都恰到好处的不浪费，又满足需求。

利用双指针不断的更新 i 孩子的需求下标和 j饼干的值，直到两者有其一达到了终点位置：

1. 如果当前的饼干不满足孩子的胃口，那么把 j++ 寻找下一个饼干，不用担心这个饼干被浪费，因为这个饼干更不可能满足下一个孩子（胃口更大）。
2. 如果满足，那么 i++; j++; count++ 记录当前的成功数量，继续寻找下一个孩子和下一个饼干。

let findContentChildren = function (g, s) {
  g.sort((a, b) => a - b)
  s.sort((a, b) => a - b)

  let i = 0
  let j = 0

  let count = 0
  while (j < s.length && i < g.length) {
    let need = g[i]
    let cookie = s[j]
    if (cookie >= need) {
      count++
      i++
      j++
    } else {
      j++
    }
  }
  return count
}

滑动窗口问题

无重复字符的最长子串-3

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

---

这题是比较典型的滑动窗口问题，定义一个左边界 left 和一个右边界 right，形成一个窗口，并且在这个窗口中保证不出现重复的字符串。

这需要用到一个新的变量 freqMap，用来记录窗口中的字母出现的频率数。在此基础上，先尝试取窗口的右边界再右边一个位置的值，也就是 str[right + 1]，然后拿这个值去 freqMap 中查找：

1. 这个值没有出现过，那就直接把 right ++，扩大窗口右边界。
2. 如果这个值出现过，那么把 left ++，缩进左边界，并且记得把 str[left] 位置的值在 freqMap 中减掉。

循环条件是 left < str.length，允许左边界一直滑动到字符串的右界。

let lengthOfLongestSubstring = function (str) {
  let n = str.length
  // 滑动窗口为s[left...right]
  let left = 0
  let right = -1
  let freqMap = {} // 记录当前子串中下标对应的出现频率
  let max = 0 // 找到的满足条件子串的最长长度

  while (left < n) {
    let nextLetter = str[right + 1]
    if (!freqMap[nextLetter] && nextLetter !== undefined) {
      freqMap[nextLetter] = 1
      right++
    } else {
      freqMap[str[left]] = 0
      left++
    }
    max = Math.max(max, right - left + 1)
  }
  return max
}

参考链接

https://juejin.cn/post/6847009772500156429